


Using python it is relatively easy to program: That is all there is to this method! To calculate the solution ten to hundreds of times and you can solve for x. In Gauss-Seidel method, we then split the A matrix into Upper (U) and Lower (L) matrices (the lower matrix in this case also contains the diagonal), then iterate using the following method: The method is fairly straight forward, given a standard system of linear equations, Ax = b. Where, A is a matrix (often representing a series of equations), x is a vector of x variables (Gauss-Seidel method is used to solve this vector) and b is the solution vector. Gauss-Seidel method is similar to Jacobi’s Method, both being iterative methods for solving systems of linear equations, but Gauss-Seidel converges somewhat quicker in serial applications. The beauty of this method, is if a matrix with diagonal dominance or is symmetric and positive definite, as well as an initial guess for the x values it is guaranteed to converge (it often converges even if these conditions are not met). Įxtracting the pure technical information, the Gauss-Seidel Method is an iterative method, where given Ax = b and A and b are known, we can determine the x values. Though it can be applied to any matrix with non-zero elements on the diagonals, convergence is only guaranteed if the matrix is either diagonally dominant, or symmetric and positive definite. It is named after the German mathematicians Carl Friedrich Gauss and Philipp Ludwig von Seidel, and is similar to the Jacobi method. What mistakes did I make? I think it is in TriSolve method since if I replaced it with regular LU solver such as (np.linalg.solve) it works.Also known as the Liebmann method or the method of successive displacement, is an iterative method used to solve a linear system of equations. Below is the same implementation in MATLAB which works: function x = gSeidel(A,B,N) For some reason it is not converging even after 50000 iterations to the solution even when the matrix A is strict diagonal dominant.
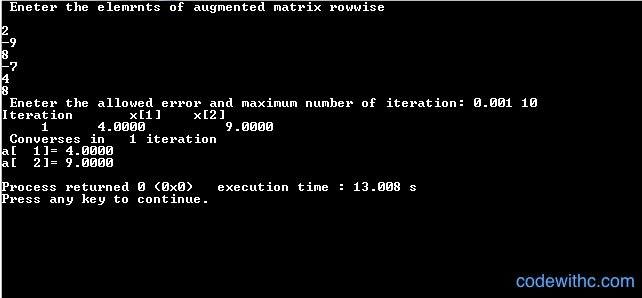
#O(n) per iteration, so overall O(nN), good for large SPD/SDD matricesĪ = np.array(,])Īns = is my Gauss-Seidel method in Python. From scipy.linalg import solve_triangular as triSolve


 0 kommentar(er)
0 kommentar(er)
